√Teori Peluang - Info Lecak
Akan tetapi sebelum membahas lebih jauh tentang Teori Peluang, tidak ada salahnya kami ucapkan selamat datang ke situs Info Lecak, sebuah situs yang berisi berbagai informasi dan tutorial. Seperti salah satunya informasi mengenai Teori Peluang. Oke yuk langsung disimak ulasan lengkapnya dibawah ini.
Ulasan Lengkap Teori Peluang
Teori Peluang atau keboleh jadian atau juga dikenal sebagai probabilitas merupakan suatu cara untuk mengungkapkan pengetahuan ataupun kepercayaan jika seuah kejadian akan berlaku atau sudah terjadi.
Konsep peluang dalam ilmu matematika sudah dirumuskan dengan lebih ketat pada matematika.
Serta telah banyak dimanfaatkan secara lebih luas dalam tidak hanya pada bidang matematika atau statistika, namun juga keuangan, sains dan juga filsafat. Selengkapnya mengenai teori peluang simak pembahasan berikut ini.
Teori Peluang
Peluang merupakan sebuah nilai antara 0 hingga 1 yang menggambarkan kemungkinan pada sebuah peristiwa yang akan terjadi.
- Suatu Eksperimen merupakan pengamatan atas beberapa kegiatan ataupun sebuah pengukuran.
- Suatu hasil merupakan keluaran tertentu dari suatu eksperimen.
- Sebuah kejadian merupakan suatu kumpulan satu hasil atau lebih dari suatu eksperimen.
Beberapa kejadian akan disebut saling bebas apabila kemunculan seebuah kejadian tidak akan memengaruhi kemunculan kejadian yang lainnya.
Dan untuk membahas lebih lanjut mengenai teori peluang, kita akan berikan beberapa hal yang berhubungan teori peluang.
Diantaranya yaitu: kejadian majemuk, aturan perkalian dan faktorial, permutasi, kombinasi dan Binomial Newton, percobaan ruang sampel dan peluang suatu kejadian, serta peluang kejadian majemuk.
Simak artikel ini sampai selesai ya.
Untuk memahami teori peluang, akan kami berikan ilustrasi agar memudahkan proses pemahaman kalin. Berikut ilustrasinya.
Apabila kalian diperintah oleh ibu kalian untuk merapikan bola warna-warni yang kalian punya ke dalam kotak mainan.
Tetapi secara tiba-tiba, adik kalian yang masih kecil minta diambilkan bola. Secara acak, kalian akan mengambil kembali bola tersebut kan?.
Nah, peluang terambilnya bola warna biru serta merah kira-kira ada berapa ya guys? Kejadian tersebutlah bisa kita jawab dengan cara mempelajari materi kejadian majemuk di dalam teori peluang matematika.
Simak cara untuk mengetahui peluangnya di bawah ini!
Kejadian majemuk adalah jika terdapat suatu kejadian atau percobaan yang berlangsung lebih dari satu kali sehingga menghasilkan kejadian baru, di mana kejadian baru tersebutlah yang disebut sebagai kejadian majemuk.
Adapun beberapa kejadian yang dikatakan sebagai kejadian majemuk, diantaranya yaitu:
1. Dua Kejadian Sembarang
Dalam dua kejadian sembarang A serta B dalam ruang sampel S, maka akan berlaku rumus:
P (A ∪ B) = P (A) + P (B) – P (A ∩ B)
Sebagai:
Diketahui dari 45 siswa dalam suatu kelas, terdapat 28 siswa yang suka pada mapel Matematika, 22 siswa suka pada mapel bahasa Inggris, serta sisa 10 siswa suka kedua-duanya.
Apabila seorang siswa dipilih secara acak, maka tentukan peluang siswa yang terpilih merupakan siswa yang menyukai Matematika ataupun bahasa Inggris!
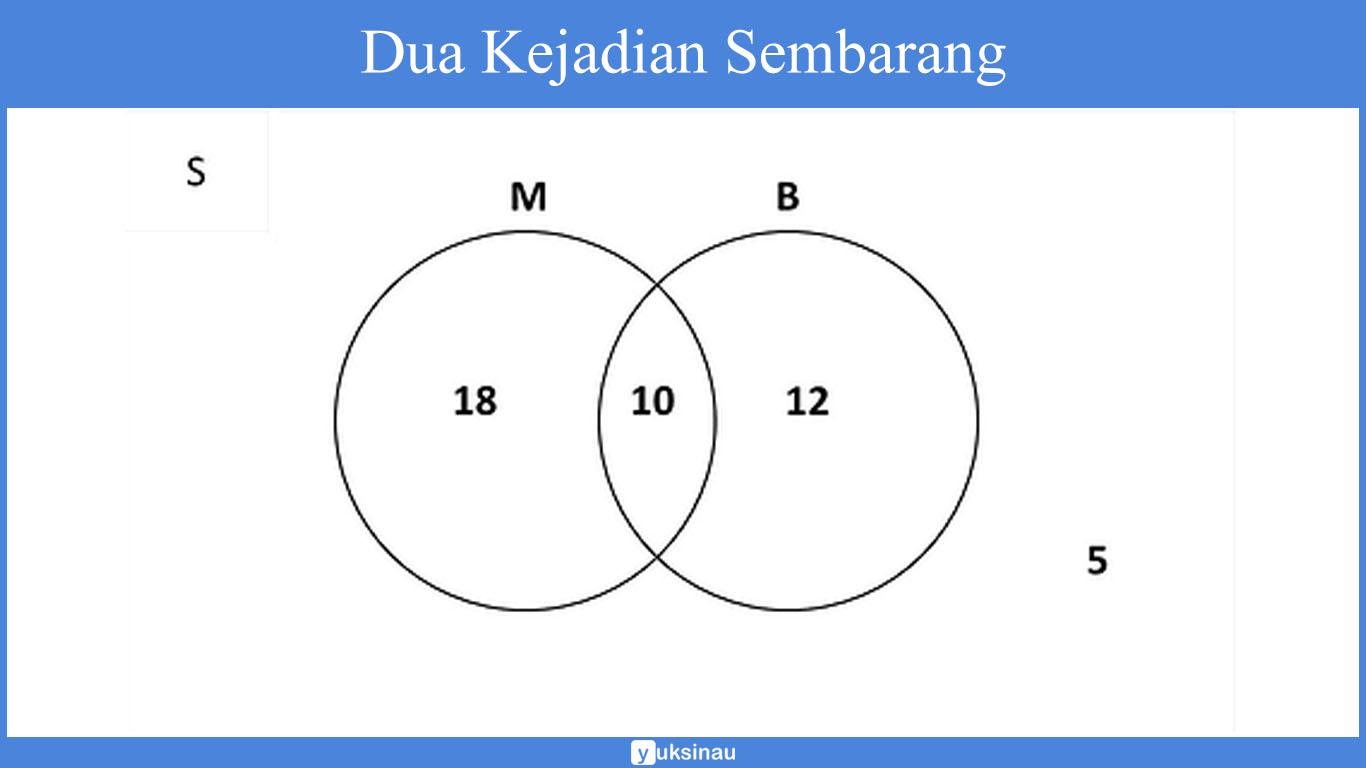
Diketahui:
- n(S) = 45
- Suka Matematika, n(M) = 28
- Suka Bahasa Inggris, n(B) = 22
- Suka keduanya, n(M ∩ B ) = 10
Jawab:
- n(S) = 45
- Suka Matematika, n(M) = 28
- Suka Bahasa Inggris, n(B) = 22
- Suka keduanya, n(M ∩ B ) = 10
Peluang di mana akan terpilih yang suka Matematika atau Bahasa Inggris adalah:
P (M ∪ B) = P (M) + P (B) – P (M ∩ B)
= 28/45 + 22/45 – 10/45
= 40/ 45
= 8/ 9
2. Komplemen Suatu Kejadian
Adapun rumus untuk mencari komplemen pada suatu kejadian, yaitu:
P (Ac) = 1 – P (A)
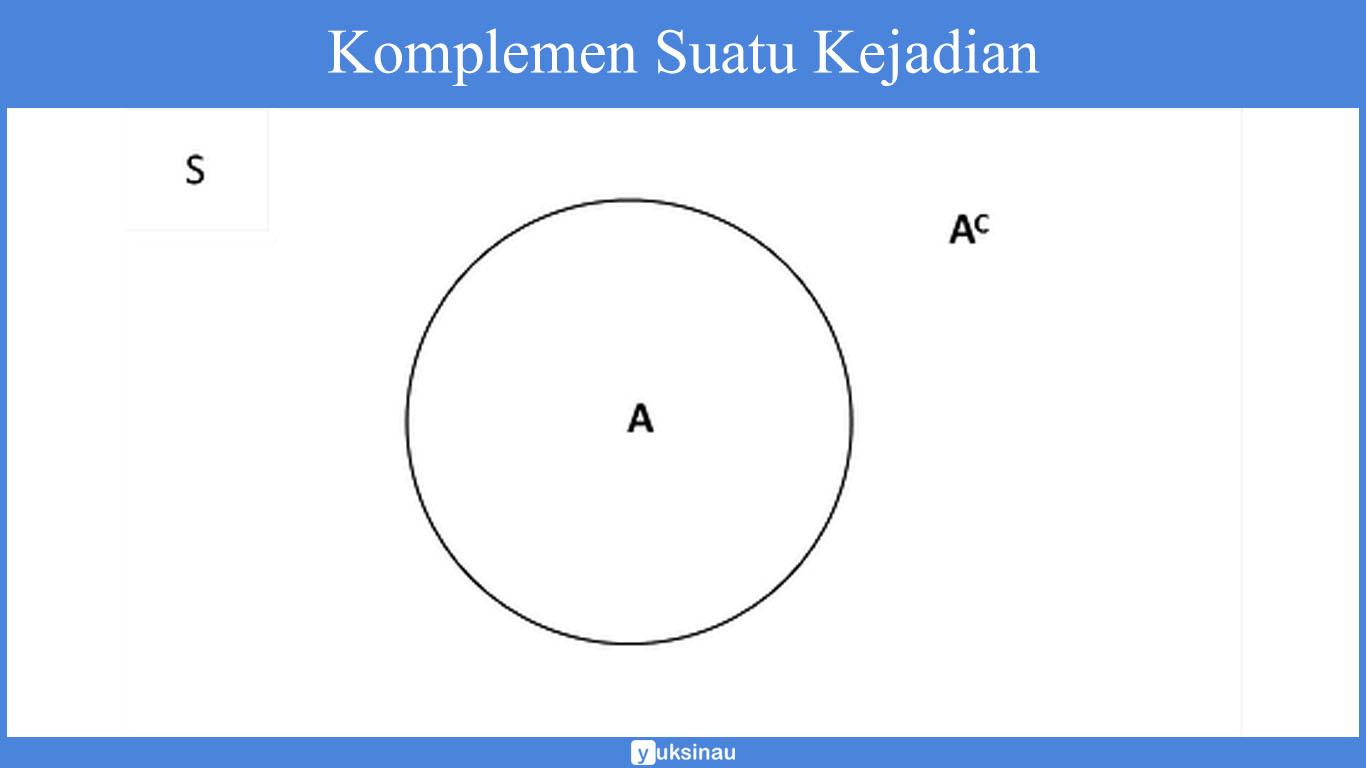
Sebagai contoh:
Suatu dadu dilempar sekali ke atas, maka hitunglah peluang munculnya mata dadu lebih dari dua.
Jawab:
Suatu dadu dilempar sekali, sehingga n (S) = 6
Apabila A = {mata dadu lebih dari sama dengan 2}
Maka dari itu, Ac = { mata dadu kurang dari atau sama dengan 2 } = {1, 2}, n(Ac) = 2
P (Ac) = n(Ac)/ n(S) = 2/ 6 = 1/ 3
Sehingga, P (A) = 1 – P (Ac)
= 1 – 1/3
= 2/ 3
Sehingga, peluang munculnya mata dadu lebih dari 2 yaitu 2/3.
3. Dua Kejadian Saling Lepas
Adapun rumus untuk menentukan dua kejadian saling lepas, yaitu:
P (A ∪ B) = P(A) + P (B)
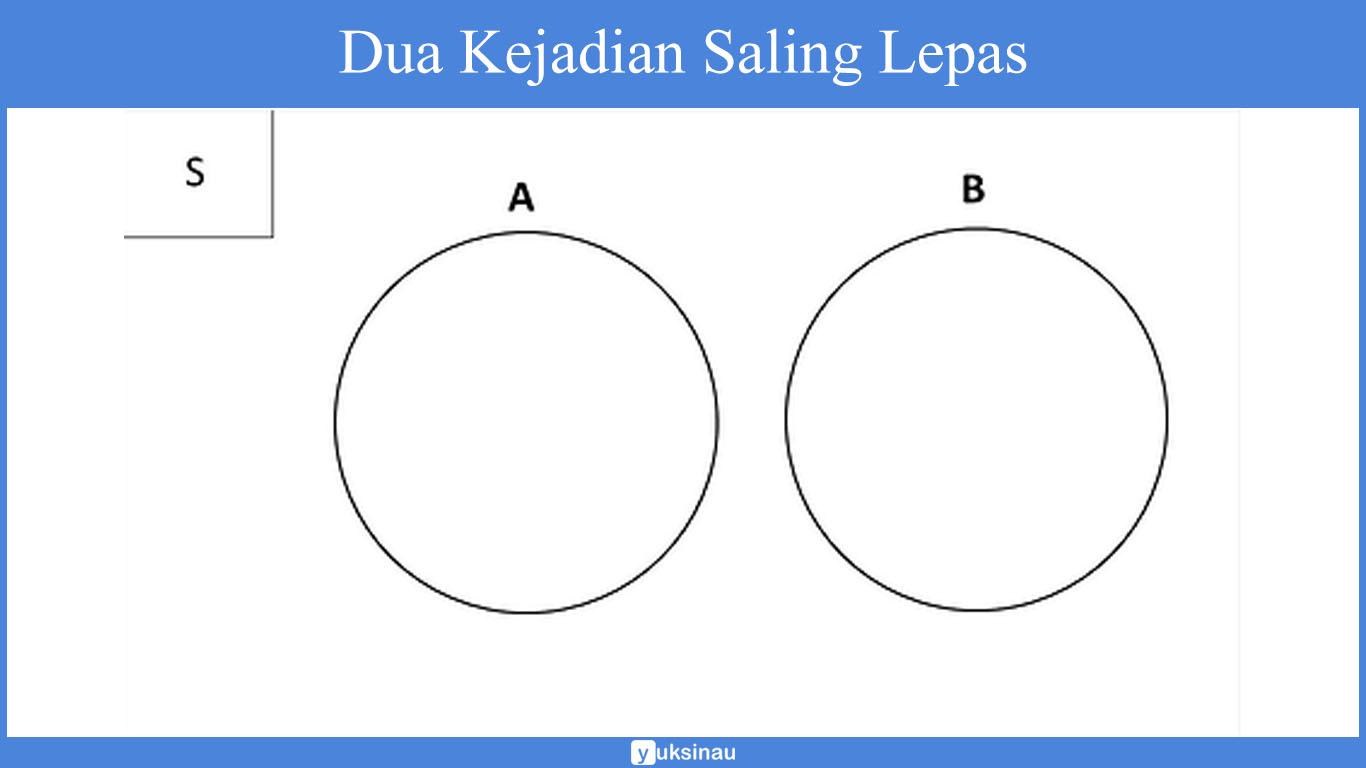
Contoh:
Pada pelemparan satu dadu bermata 6, berapakah peluang untuk memperoleh dadu dengan mata 1 atau 3 ?
Jawab:
A = {1}, B = {3}
n(A) = 1, n(B) = 1
Peluang untuk memperoleh dadu mata 1 atau 3, yaitu:
P (A ∪ B) = P(A) + P (B)
P (A ∪ B) = 1/ 6 + 1/ 6 = 2/ 6 = 1/ 3
4. Dua Kejadian Saling Bebas
Kejadian A dan B dikatakan saling bebas jika kejadian A tidak mempengaruhi kejadian B dan kejadian B tidak mempengaruhi kejadian A. Dirumuskan:
P (A ∩ B) = P (A) X P (B)
Contoh:
Apabila peluang Gilang bisa menyelesaikan sebuah soal yaitu 0,4 serta peluang Putra bisa menyelesaikan soal yang sama yaitu 0,3 maka peluang mereka berdua bisa menyelesaikan soal tersebut yaitu …
Jawab:
P(A) = 0,4
P(B) = 0,3
Peluang Gilang dan Putra bisa menyelesaikan soal adalah:
P (A ∩ B) = P (A) X P (B) = 0,4 x 0,3 = 0,12
5. Dua Kejadian Bersyarat
Apabila kejadian A serta B tidak saling bebas, kejadian B dipengaruhi oleh kejadian A ataupun kejadian B dengan syarat A, maka dapat kita rumuskan menjadi:
P(B | A) = P (A ∩ B)/ P(A) atau P (A ∩ B) = P(A) x P(B | A)
Sebagai contoh:
Suatu dadu dilempar sekali. Hitunglah peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima terlebih dahulu.
Jawab:
Diketahui;
S = {1, 2, 3, 4, 5, 6}, n(S) = 6
A = Kejadian munculnya angka prima
A = {2, 3, 5}, n(A) = 3
P(A) = n(A)/ n(S) = 3/ 6 = 1/ 2
B = Kejadian muncul mata dadu ganjil
B = {1, 3, 5}
P(A) = n(A)/ n(S) = 3/ 6 = 1/ 2
Peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima terlebih dahulu adalah:
P(B | A) = P (A ∩ B)/ P(A) = 1/4 / 1/2 = 1/2
Sesudah kalian selesai mempelajari semua peluang kejadian majemuk, maka bisa kita simpulkan bahwa:
Rumus Formula Kejadian Majemuk
| No. | Jenis Kejadian Majemuk | Rumus |
| 1 | Dua Kejadian Sembarang | P (A ∪ B) = P (A) + P (B) – P (A ∩ B) |
| 2 | Komplemen Suatu Kejadian | P (Ac) = 1 – P (A) |
| 3 | Dua Kejadian Saling Lepas | P (A ∪ B) = P(A) + P (B) |
| 4 | Dua Kejadian Saling Bebas | P (A ∩ B) = P (A) X P (B) |
| 5 | Dua Kejadian Bersyarat | P(B | A) = P (A ∩ B)/ P(A) atau P (A ∩ B) = P(A) x P(B | A) |
Melanjutkan teori peluang, di bawah ini akan kami jelaskan mengenai aturan perkalian dan faktorial, permutasi, kombinasi dan Binomial Newton, percobaan ruang sampel dan peluang suatu kejadian, dan peluang kejadian majemuk. Perhatikan baik-baik ya.
Pernahkah kalian hendak pergi ke suatu tempat, namun ternyata langit mendung, tampak gelap, hingga angin bertiup lebih kencang dari biasanya?
Lalu, kalian berpikir kemungkinan besar sebentar lagi akan turun hujan.
Nah, tanpa kalian sadari, sebetulnya kalian sudah menerapkan teori peluang dalam kehidupan sehari hari lho.
Nah, agar kita lebih paham mengenai teori peluang ini yuk kita pelajari aturan perkalian dan faktorial dalam teori peluang.
Di dalam kita mempelajari teori peluang, kalin juga harus mengetahui tentang kaidah pencacahan.
Yang berarti sebuah ilmu yang berhubugan dengan menentukan atau mencari banyaknya cara suatu percobaan bisa terjadi.
Hal dasar yang harus dapat kalian pahami dalam mempelajari kaidah pencacahan antara lain yaitu aturan perkalian, faktorial, serta permutasi.
A. Aturan Perkalian
Apabila sebuah kejadian bisa terjadi dalam m cara serta kejadian kedua bisa terjadi dalam n cara, maka pasangan kejadian bisa terjadi:
Rumus Formula Aturan Perkalian
m x n cara
Keterangan:
m: merupakan kejadian pertaman.
n: merupakan kejadian kedua.
Prinsip ini bisa digenerelasasikan dalam memasukan banyak kejadian yang bisa berlangsung di dalam n1,n2,n3,…nk cara.
Banyaknya k kejadian bisa berlangsung atau terjadi dalam n1.n2.n3.…nk cara.
Sebagai contoh:
Gilang memiliki 3 celana berwarna hitam, biru dan juga merah serta memiliki 4 kaos berwarna biru, merah, kuning, dan juga merah muda. Berapa banyak pasang cara Gilang untuk memilih celana serta baju?
Jawab:
n1 = Kejadian 1 (celana) = 3
n2 = Kejadian 2 (kaos) = 4
Banyak pasang cara Gilang dalam memilih celana dan baju adalah:
n1 × n2 = 3 × 4 = 12 cara.
B. Faktorial
Dalam pelajaran matematika, faktorial dari bilangan asli n merupakan suatu hasil perkalian antara bilangan bulat positif yang kurang dari atau sama dengan n.
Faktorial juga biasa dinotasikan dengan penggunaan huruf: n! dan dibaca n faktorial.
Bentuk dari faktorial, yakni:
Rumus Formula Faktorial
n! = n . (n -1) . (n – 2) . ….. (n – n + 1)
yang mana, untuk 0! = 1! = 1, sehingga akan menjadi:
2! = 2.1 = 2
3! = 3.2.1 = 6
4! = 4.3.2.1 = 24
5! = 5.4.3.2.1 = 120
dan begitu juga seterusnya.
Sebagai contoh:
Tentukan faktorial nilai dari:
1. 10!.3!/ 81.4! =
2. 6! + 4!/ 5! – 7!/ 5! =
Jawab:

Sesudah kita belajar mengenai aturan perkalian sera faktorial dalam teori peluang, maka selanjutnya kita akan membahas mengenai permutasi.
Permutasi merupakan suatu susunan unsur berbeda yang terbentuk dari n unsur, diambil dari n unsur ataupun sebagian unsur.
Permutasi bisa dikelompokkan menjadi beberapa macam.
Dan di dalam kali ini kita akan belajar mengenai jenis permutasi dalam teori peluang. Kira-kira apa saja ya jenis-jenis permutasi tersbut? Selengkapnya simak baik-baik ulasan di bawah ini.
Rumus Formula Permutasi
| No. | Jenis Permutasi | Rumus |
| 1 | Permutasi dari n elemen, tiap permutasi terdiri dari n elemen | P(n,n) = n! atau nPn = n! |
| 2 | Permutasi n elemen, tiap permutasi terdiri dari r unsur darin elemen r < n. | P(n-r) = nPr = Pnr = n!/ (n – r)! |
| 3 | Permutasi dari n unsur yang mengandung p.q serta r unsur yang sama. | P(n,k1,k2, kt) = n!/ k1!k2! … kt! |
| 4 | Permutasi siklis. | nPsiklis = (n – 1)! |
| 5 | Permutasi berulang dari n unsur, tipe permutasi terdiri dari k unsur. | Pn = nk |
1. Permutasi dari n elemen, tiap permutasi terdiri dari n elemen
Jika ada unsur yang berbeda diambil n unsur, maka banyaknya susunan (permutasi) yang berbeda dari n unsur tersebut adalah
P(n,n) = n! atau nPn = n!
Sebagai contoh:
Dalam menyambut suatu pertemuan delegasi negara yang dihadiri sebanyak lima negara, panitia akan kemudian memasang kelima bendera dari lima negara yang nantinya akan hadir.
Banyaknya cara panitia dakam menyusun kelima bendera tersebut terdapat berapa cara?
Jawab:
Dari lima bendera yang tersedia, itu artinya n = 5, maka banyak susunan bendera yang mungkin adalah:
5! = 5.4.3.2.1 = 120 cara.
2. Permutasi n elemen, masing-masing permutasi terdiri dari r unsur dari n elemen dengan r ≤ n
Untuk seluruh bilangan positif n serta r, dengan r ≤ n, banyaknya permutasi dari n objek yang diambil r objek dalam satu waktu yaitu:
P(n-r) = nPr = Pnr = n!/ (n – r)!
*syarat urutan perlu diperhatikan
Contoh:
Banyak cara dalam memilih seorang ketua, sekertaris dan juga bendahara dari 8 siswa yang tersedia ialah…
Jawab:
Diketahui:
- Banyak siswa, n = 8
- Ketua, sekretaris serta bendahara (banyak pilihan objek), r = 3
Sehingga:
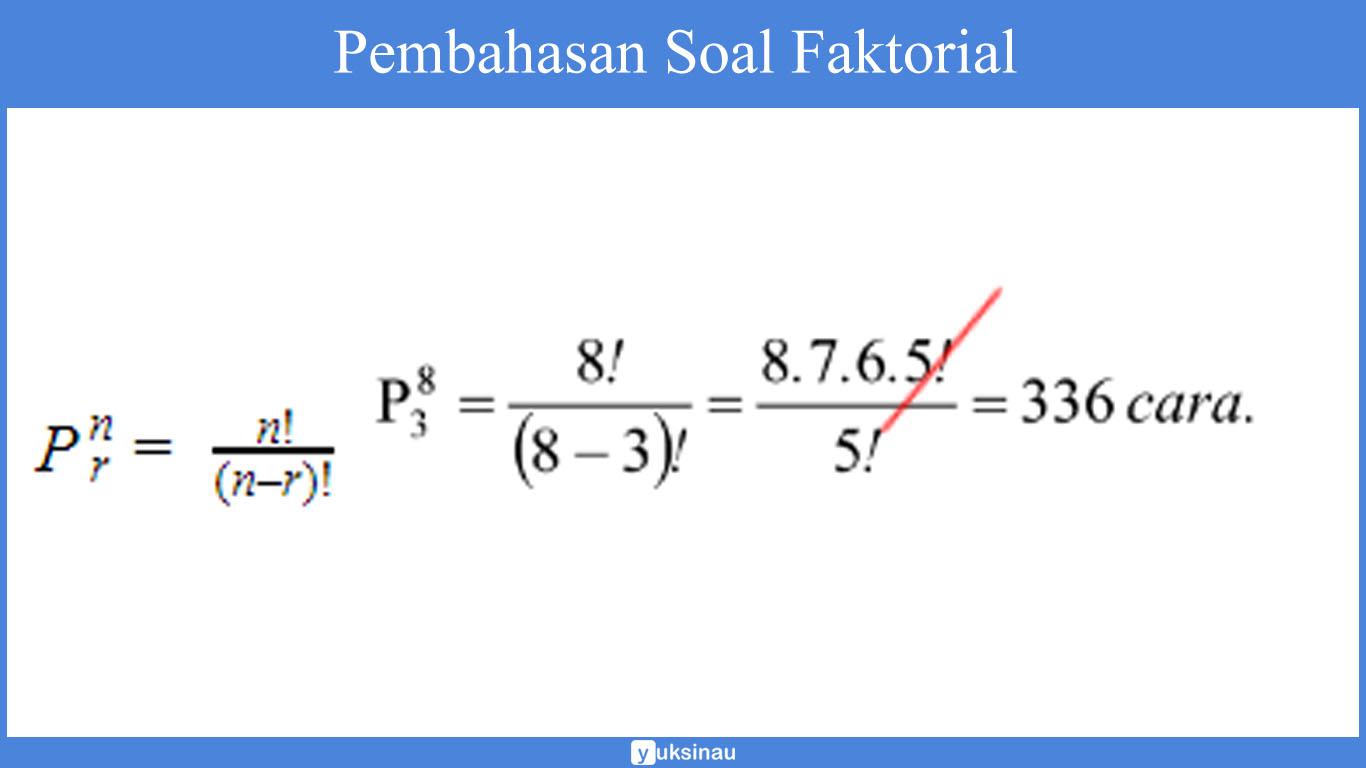
3. Permutasi dari n unsur yang mengandung p.q dan r unsur yang sama
Rumus yang digunakan adalah:
P(n,k1,k2, kt) = n!/ k1!k2! … kt!
Keterangan:
n = merupakan banyaknya elemen seluruhnya
k1 = merupakan banyaknya elemen kelompok 1 yang sama
k2 = merupakan banyaknya elemen kelompok 2 yang sama
…
kt = merupakan banyaknya elemen kelompok kt yang sama
t = 1,2,3,…dst.
Sebagai contoh:
Banyaknya cara dalam menyusun dari kata ”BASSABASSI” yaitu…
Jawab:
Dari kata ”BASSABASSI”, banyak huruf (n) adalah = 10
Diketahui:
k1 = huruf B = 2
k2 = huruf A = 3
k3 = huruf S = 4
k4 = huruf I = 1
Penyelesaian:
P(10,2,3,4,2) = 10!/ 2!.3!.4!.2! = 10.9.8.7.6.5.4!/ 2.1.3.2.1.4!.2.1 = 1260 cara.
4. Permutasi Siklis
Permutasi siklis merupakan permutasi melingkar (atau untuk urutan melingkar).
Rumus yang digunakan dalam permutasi siklis adalah:
nPsiklis = (n – 1)!
Sebagai contoh:
Dari 5 orang anggota keluarga akan segera duduk mengelilingi suatu meja bundar, banyaknya cara untuk susunan yang bisa dibuat dari 5 orang tersebut yaitu…
Jawab:
Banyak orang (n) = 5, sehingga:
5Psiklis = (5 – 1)! = 4! = 4.3.2.1 = 24 cara.
5. Permutasi berulang dari n unsur, tipe permutasi terdiri dari k unsur
Rumus yang digunakan adalah:
Pn = nk
Contoh:
Banyaknya susunan 3 bilangan dari angka-angka 1, 2, 3, 4, 5 dan 6 ialah…
Jawab:
Banyak susunan 3 bilangan, itu artinya bilangan ratusan, k = 3
Banyak angka yang akan disusun adalah n = 6
Banyak susunan 3 bilangan dari angka 1, 2, 3, 4, 5, serta 6:
P6 = 63 = 216 susunan.
Selanjutnya kita akan fokus ke pembahasan kombinasi dan binomial Newton. Dan kita akan bahas satu persatu ya. Simak baik-baik ulasan di bawah ini.
A. Kombinasi
Kombinasi merupakan suatu pemilihan objek tanpa memperhatikan urutannya.
Kombinasi pada umumnya dinotasikan seperti:
Cnr = nCr
Untuk seluruh bilangan positif n serta r, dengan r ≤ n r ≤ n, banyaknya kombinasi r objek yang diambil dari n objek dalam waktu yang sama, adalah:
Rumus atau Formula Kombinasi
nCr = n!/ (n-r)!r!
Sebagai contoh:
Soal 1.
Banyak cara untuk memilih pemain inti dari suatu tim basket dari 9 orang yaitu…
Jawab:
Diketahui:
Suatu tim basket terdiri atas 5 orang, r = 5
Banyak orang yang bisa dipilih adalah n = 9
Banyak cara untuk memilih pemain inti dari suatu tim basket adalah:
nCr= 9!/ (9-5)!5! = 9.8.7.6.5!/ 4!.5! = 9.8.7.6/4.3.2.1 = 126 cara
Soal 2.
Dari total 4 penyanyi sopran serta 5 penyanyi alto akan dipilih empat orang pengurus paduan suara.
Berapa banyak pilihan yang berbeda yang nantinya akan didapatkan apabila dipilih 2 orang penyanyi sopran serta 2 orang penyanyi alto?
Jawab:
Banyaknya cara dalam memilih pengurus paduan suara adalah:
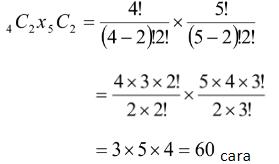
B. Binomial Newton
Binomial Newton merupakan suatu teorema yang menerangkan tentang mengenai pengembangan eksponen dari penjumlahan antara dua variabel (binomial).
Dalam Binomial Newton memakai koefisien-koefisien (a + b)n.
Sebagai contoh, n = 2 diperoleh dari: (a + b)2 = (1) a2 + 2ab + (1)b2
Koefisien-koefisien hasil penjabaran (a + b)2 merupakan 1, 2, 1 yang senilai dengan C(2,0) serta C(2,2) bisa kita tuliskan menjadi:
(a + b)2 = C(2,0) a2 + C(2,1) + ab + C(2,2) b2
Rumus atau Formula Binomial Newton
Secara umum akan berlaku:
(a + b)2 = C(n,0) a2 + C(n,1) an-1 + C(n,2) an-2 + …. + C(n,r)an-r br+ C(n,n) bn
Apabila ditulis dalam notasi sigma, maka akan di dapatkan:
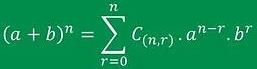
Sebagai contoh:
Suku ke-7 dari (2x + y)15 yaitu…
Jawab:
Diketahui:
n = 15
r = 7 – 1 = 6
Sehingga:
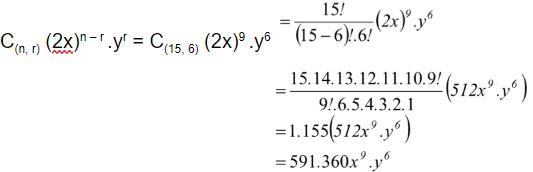
Dan yang terakhir dalam teori peluang, kita akan mempelajari mengenai percobaan, ruang sampel dan peluang menghitung suatu kejadian. Yuk, kita bahas satu persatu, simak baik-baik ya.
A. Percobaan
Sifat dasar percobaan adalah:
- Pada masing-masing jenis percobaan memiliki kemungkinan hasil atau peristiwa atau kejadian yang akan terjadi.
- Hasil dari masing-masing percobaan tersebut secara pasti akan sulit ditentukan.
Ilustrasi:
| No. | Percobaan | Kemungkinan Hasil |
| 1 | Melempar satu keping mata uang logam | Muncul gambar (G) atau angka (A) |
| 2 | Melempar satu buah dadu | Muncul mata 1, 2, 3, 4, 5, dan 6. |
B. Ruang Sampel
Ruang sampel (S) adalah kumpulan dari hasil yang mungkin terjadi dari suatu percobaan. Titik sampel adalah anggota-anggota dari ruang sampel, sedangkan kumpulan dari beberapa titik sampel disebut kejadian.
Banyak ruang sampel disimbolkan dengan n(S).
Sebagai contoh:
Satu buah koin di lempar sebanyak 3 kali, maka dari itu ruang sampel daserta banyaknya sampel dari percobaan pelemparan koin tersebut ialah…
Jawab:
Kemungkinan:
- Koin ke-1 : A A A G A G G G
- Koin ke-2 : A A G A G A G G
- Koin ke-3 : A G A A G G A G
Maka;
S = {(AAA), (AAG), (AGA), (GAA), (AGG), (GAG), (GGA), (GGG)}
n(S) = 8
C. Peluang Kejadian
Sebagai cotoh S merupakan ruang sampel dari sebuah percobaan dengan masing-masing anggota S mempunyai kesempatan muncul yang sama dan K merupakan sebuah kejadian dengan K⊂S, sehingga peluang kejadian K adalah:
Rumus atau Formula Peluang Kejadian
P(K) = n(K) / n(S)
dengan 0 ≤ P(K) ≤ 1,
Ketarangan:
n(K): merupakan banyak anggota dalam kejadian K.
n(S): merupakan banyak anggota dalam himpunan ruang sampel.
Sebagai contoh:
Satu buah dadu dilempar undi satu kali, peluang munculnya angka bilangan prima yaitu…
Jawab:
Diketahui:
- Ruang sampel dadu adalah (S) = {1, 2, 3, 4, 5, 6} maka n(S) = 6
- Muncul angka prima adalah (K) = {2, 3, 5} maka n(K) = 3
Sehingga peluang munculnya angka bilangan prima adalah:
P(K) = n(K) / n(S) = 3/ 6 = 1/ 2
D. Peluang komplemen dari suatu kejadian
P(K) merupakan sautu peluang kejadian K dan juga P(Kc) = P(K’) merupakan suatu peluang kejadian bukan K, maka akan berlaku:
Rumus atau Formula Peluang komplemen dari suatu kejadian
P(K) + P(Kc) = 1
P(Kc) = 1 – P(K)
Sebagai contoh:
Peluang Gilang akan lulus ujian Matematika ialah 0,89, sehingga peluang Gilang tidak lulus ujian Matematika yaitu …
Jawab:
Diketahui:
- K = merupakan kejadian Rina lulus ujian Matematika = 0,89
- Kc = merupakan kejadian Rina tidak lulus ujian Matematika
Peluang Rina tidak lulus ujian Matematika adalah:
P(Kc) = 1 – P(K) = 1 – 0,89 = 0,11
E. Frekuensi Harapan
Frekuensi harapan merupakan banyaknya kejadian yang diharapkan bisa berlangsung atau terjadi pada sebuah percobaan.
Apabila sebuah percobaan dilakukan sebanyak n kali serta nilai kemungkinan berlangsung kejadian K pada masing-masing percobaan ialah P(K), maka frekuensi harapan kejadian K yaitu:
Rumus atau Formula Frekuensi Harapan
Fh(K) = n x P(K)
Sebagai contoh:
Satu buah dadu dilempar sebanyak 120 kali, maka frekuensi harapan munculnya mata dadu faktor dari 6 yaitu …
Jawab:
Diketahui:
- S = {1, 2, 3, 4, 5, 6}
 n(S) = 6
n(S) = 6 - K : Faktor dari 6 = {1, 2, 3, 6}
 n(A) = 4
n(A) = 4 - n = Banyak lemparan = 120
Sehingga;
P(K) = n(K) / n(S) = 4/ 6 = 2/ 3
Sehingga frekuensi harapan muncul faktor dari 6 yaitu:
Fh(K) = n x P(K) = 120 x 2/ 3 = 80 kali.
Demikianlah ulasan singkat mengenai Teori Peluang yang dapat kami sampaikan. Semoga ulasan di atas mengenai Teori Peluang dapat kalian jadikan sebagai bahan belajar kalian.
The post Teori Peluang appeared first on Tuliskan.
Sekian dulu ulasan mengenai Teori Peluang yang bisa kami sampaikan untuk sobat semuanya. Kami ucapkan banyak terima kasih karena sudah mengunjungi situs infolecak. blogspot. com dan membaca urian diatas hingga selesai. Harapannya apa yang kami sampaikan diatas dapat menambah wawasan kita semuanya, terlebih untuk Anda yang memang sedang mencarinya. Jangan lupa bahagia dan sampai jumpa di postingan selanjutnya.
Post a Comment for "√Teori Peluang - Info Lecak"